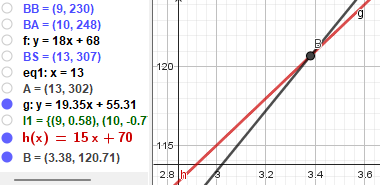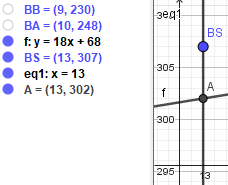
 Som i kan se forslår mit program at linjen, der er vores forslag til prismodel
kan beskrives ved regnestykket
$$y=A(x)=18x+68$$
(den bruger godt nok bogstavet "f", men vi kan kalde det hvad der passer os).
De to tal der indgår i regnestykket beskriver henholdsvis kilometer-prisen, dvs.
at det koster 18kr. for hver kørt kilometer og at startgebyret er 68 kr., dvs.
hvor meget vi skal betale for at sætte os ind i taxaen.
Som i kan se forslår mit program at linjen, der er vores forslag til prismodel
kan beskrives ved regnestykket
$$y=A(x)=18x+68$$
(den bruger godt nok bogstavet "f", men vi kan kalde det hvad der passer os).
De to tal der indgår i regnestykket beskriver henholdsvis kilometer-prisen, dvs.
at det koster 18kr. for hver kørt kilometer og at startgebyret er 68 kr., dvs.
hvor meget vi skal betale for at sætte os ind i taxaen.


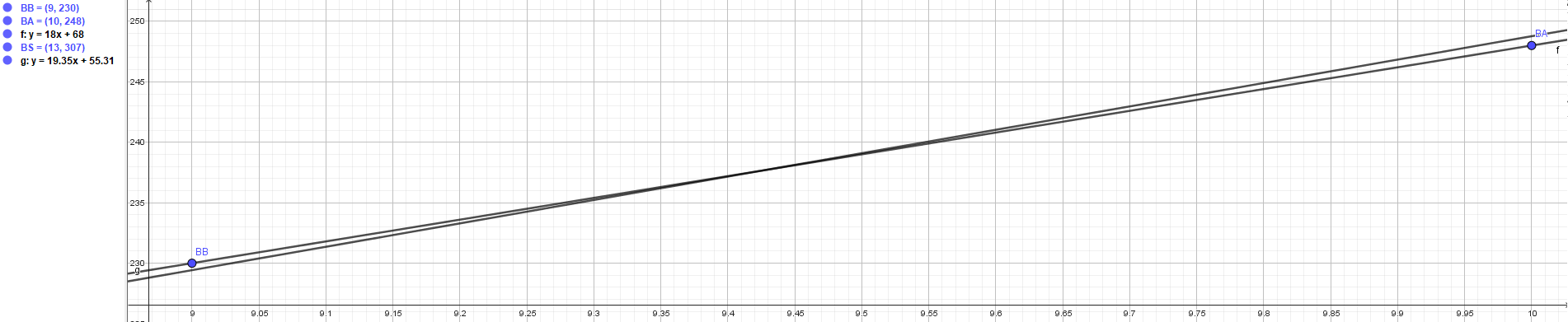 og den går faktisk imellem vores to første punkter, så nu ligger ingen af vores
punkter på linjen. Men spørgsmålet er, hvor meget afviger hvert af punkterne?
Lad os prøve at beregne forskellen mellem prismodellens værdi og den faktiske
pris.
$$230-A(9)=230-(19.35⋅9+55.31)=0.54$$
dvs. at turen til Bagsværd koster 54 øre mere end forventet.
$$248-A(10)=248-(19.35⋅10+55.31)=-0.81$$
dvs. at turen til Albertslund koster 81 øre mindre end forventet.
$$307-A(13)=307-(19.35⋅13+55.31)=0.14$$
dvs. at turen til Stenløse er gået fra at være 5 kr. dyrere end forventet til
kun at være 14 øre dyrere. Alt i alt har vores "bedste linje" gjort at vi rammer
lidt ved siden af ved de to første rejser, men den har markant forbedret den
tredje. Det vi lige har beregnet er de såkalde "residualer", som er afvigelserne
mellem modellen og vores punkter.
og den går faktisk imellem vores to første punkter, så nu ligger ingen af vores
punkter på linjen. Men spørgsmålet er, hvor meget afviger hvert af punkterne?
Lad os prøve at beregne forskellen mellem prismodellens værdi og den faktiske
pris.
$$230-A(9)=230-(19.35⋅9+55.31)=0.54$$
dvs. at turen til Bagsværd koster 54 øre mere end forventet.
$$248-A(10)=248-(19.35⋅10+55.31)=-0.81$$
dvs. at turen til Albertslund koster 81 øre mindre end forventet.
$$307-A(13)=307-(19.35⋅13+55.31)=0.14$$
dvs. at turen til Stenløse er gået fra at være 5 kr. dyrere end forventet til
kun at være 14 øre dyrere. Alt i alt har vores "bedste linje" gjort at vi rammer
lidt ved siden af ved de to første rejser, men den har markant forbedret den
tredje. Det vi lige har beregnet er de såkalde "residualer", som er afvigelserne
mellem modellen og vores punkter.
 Skæringspunktet \(A=(2.31,100)\) betyder at vi kan køre 2.31 km for de 100 kr.
og hvis vi skal videre må vi gå eller tage flere penge med. Nogle gange er det
upraktisk at løse ligningen geometrisk, og man skal også kunne løse ligninger
i hånden, så derfor kan man også opstille ligningen algebraisk som
$$100=A(x)=19.35x+55.31$$
Løsningen forgår ved at finde de x'er der opfylder den og det sker i praksis
ved at manipulere ligningen indtil at x står alene.
\begin{align}
&&100=&19.35x+55.31\\
\iff&&100-55.31=&19.35x\cancel{+55.31-55.31}\\
\iff&&\frac{44.69}{19.35}=&\frac{\cancel{19.35}x}{\cancel{19.35}}\\
\iff&&x=&\frac{44.69}{19.35}\approx2.31
\end{align}
her kan vi igen se at vi kan køre 2.31 km for de 100 kr. Hvis det viser sig at
vi ikke har råd til vores tur kan det være at vi skal vælge et andet taxaselskab.
Jeg har fundet et andet selskab der hedder Drivr, hvor kilometerprisen er 15
kr. og startgebyret er 70 kr. og for at sammenligne dem finder skæringspunktet
mellem deres grafer. Det er ret oplagt at gøre geometrisk hvor vi tegner graferne
for de to selskaber og bruger vores matematikværktøj til at finde det for os
Skæringspunktet \(A=(2.31,100)\) betyder at vi kan køre 2.31 km for de 100 kr.
og hvis vi skal videre må vi gå eller tage flere penge med. Nogle gange er det
upraktisk at løse ligningen geometrisk, og man skal også kunne løse ligninger
i hånden, så derfor kan man også opstille ligningen algebraisk som
$$100=A(x)=19.35x+55.31$$
Løsningen forgår ved at finde de x'er der opfylder den og det sker i praksis
ved at manipulere ligningen indtil at x står alene.
\begin{align}
&&100=&19.35x+55.31\\
\iff&&100-55.31=&19.35x\cancel{+55.31-55.31}\\
\iff&&\frac{44.69}{19.35}=&\frac{\cancel{19.35}x}{\cancel{19.35}}\\
\iff&&x=&\frac{44.69}{19.35}\approx2.31
\end{align}
her kan vi igen se at vi kan køre 2.31 km for de 100 kr. Hvis det viser sig at
vi ikke har råd til vores tur kan det være at vi skal vælge et andet taxaselskab.
Jeg har fundet et andet selskab der hedder Drivr, hvor kilometerprisen er 15
kr. og startgebyret er 70 kr. og for at sammenligne dem finder skæringspunktet
mellem deres grafer. Det er ret oplagt at gøre geometrisk hvor vi tegner graferne
for de to selskaber og bruger vores matematikværktøj til at finde det for os